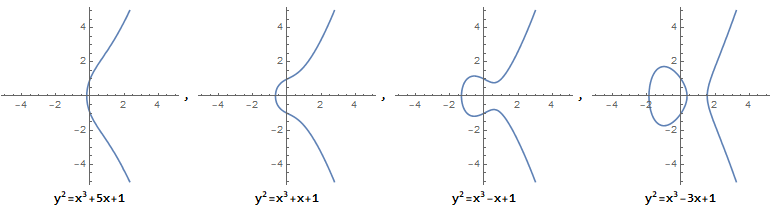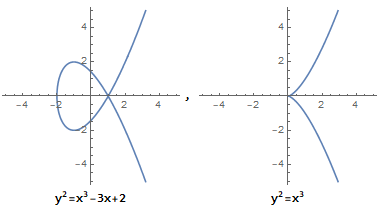豌豆

一、技术债务的AI困境：效率剪刀差加剧

生成式AI的普及正在技术领域制造显著的"效率剪刀差"现象。在技术债务低于警戒线的代码库中，AI工具可提升40%以上的开发效率，这种增效作用如同代码加速引擎。但当面对以下特征的遗留系统时，AI的赋能效果往往呈现出断崖式下跌的现象：

• 混沌架构：超过3层的嵌套控制流、环状依赖关系
• 暗盒逻辑：缺乏文档的定制化框架、魔数遍布的业务规则
• 脆弱基座：存在历史补丁超过原始代码量的核心模块

这种技术鸿沟导致企业陷入双重困境：新项目因AI加持加速迭代，而旧系统维护成本却指数级增长。某金融科技公司的实践数据显示，其新微服务模块开发周期缩短至2周，而核心交易系统的AI辅助成功率不足15%。

结构化绑定定义及用法

所谓"结构化绑定", 即将指定的名称绑定到初始化器的子对象或元素上。比如有如下结构体：

1
2
3
4

struct Student {
  int age;
  std::string name;
};

那么有如下写法,直接把该结构体的成员绑定到新的变量名上：

1
2

Student st{18, "Tom"};
auto [a, n] = st;  //auto a=n.age, auto n=s.name

结构化绑定支持的方式：

1
2
3

auto [ident-list] = expression;
auto [ident-list] {expression};
auto [ident-list](expression);

auto 前后可以使用 const alignas 和 & 修饰。

结构化绑定可以用在 数组(array)、类元组(tuple-like)和成员变量上(data members)。

1
2
3
4
5
6
7
8
9
10
11
12
13

int tm[3] = {1949, 10, 1};
auto [y, m, d] = tm;
std::cout << m << "/" << d << "/" << y << std::endl;

std::map<int, std::string> mp = {{1, "Name"}, {2, "Age"}};
for (const auto& [k, v] : mp) {
  std::cout << k << ": " << v << std::endl;
}

auto [it, rst] = mp.insert({1, "Type"});
if (!rst) {
  std::cout << "Insert Error" << std::endl;
}

这么做的好处是使得代码结构更清晰，简洁易读。

函数重载（Function Overloading）允许在同一个作用域内定义多个功能类似但参数不同的函数。这些函数可以有相同的名字，但必须有不同的参数列表（参数的数量、类型或顺序不同）。编译器通过参数列表来决定调用哪个函数。

大部分语言并不支持返回值类型的重载。包括C++。

1
2
3
4
5
6
7
8
9
10
11
12
13

// OK
std::string to_string(int i);
std::string to_string(bool b);

std::string si = to_string(42);
std::string sb = to_string(true);

// ERROR
int from_string(std::string_view s);
bool from_string(std::string_view s);

int i = from_string("42");
bool b = from_string("false");

C++ 11 的一个新特性，使我们可以实现一个 接近 函数返回值重载的功能。即 自定义转换函数
来看下面的例子：

1
2
3
4
5
6
7
8
9
10

struct to_string_t
{
    std::string_view s;  //string_view from c++17

    operator int() const; 
    operator bool() const;
};

int i = to_string_t{"42"};  //  operator int() const; 
bool b = to_string_t{"true"};  //  operator bool() const;

需要注意，编译器需要知道转换的目标类型。如 auto i = to_string_t{"42"} ，编译器不知道应该调用哪个重载。
让我们回到开始：如何将 to_string_t 作为返回值，似乎就可以完成 函数返回值重载 的功能:

Ranges 是C++20 提供的一套对范围的统一抽象和操作库。ranges 指可迭代的序列，它可以包括任何能够提供迭代器的数据结构， 如 vector, list, etc. 引入 ranges 可以使迭代的处理更简洁直观灵活。

我们知道 STL algorithms 利用迭代器对数据进行操作。比如我们需要对一个 vector 进行排序, 需要将排序的范围的迭代器做为参数传递给 sort() 方法：

1
2
3

std::vector v = {1,6,4,2,8};
std::sort(v.begin(), v.end());
std::sort(v.begin(), v.end(), std::greater());

这种写法很灵活。但更多的时候，我们是想对整个 vector 进行排序，传入迭代器反而是多余的操作了。引入 Ranges 即可简化这一操作。

1
2

std::ranges::sort(v);
std::ranges::sort(v,std::greater());

一. 引入

简单地说：enable_shared_from_this 是为了解决 在类的内部获取自己的 shared_ptr 这件事情而存在的。

众所周知，每一个对象都能通过 this 指针来访问自己的地址。this 指针也是所有成员函数的隐含参数。然而有些时候，我们需要的不仅是 this，而是一个 “this 的智能指针”。

在使用对称加密中，有一些无法避免的问题：

• 密钥如何从加密方传递给解密方。窃听者如果可以劫获密文，那么也可能劫获密钥.
• 如果窃听者破解了密钥，加密方如何将新的密钥安全地交给解密方

DH 密钥交换

解决上述问题的一种方法就是 DH 密钥交换 技术 。

DH 密钥交换全称为 Diffie-Hellman 密钥交换 ,是1976年由 Whitfiedl Diffle 和 Martin Hellman 共同发明的一种算法。使用这种方法，通信双方可以在窃听者眼皮子底下来安全地传输密码。

DH 交换的步骤如下：

ECC(Elliptic Curves Cryptography) 属于非对称加密算法的一个重要组成部分。

本文尽量简单地阐述椭圆曲线加密的原理，但需要读者有一些初级的数论与离散数学相关的知识，或者推荐简单地阅读《算法导论》第31章:数论算法。

椭圆曲线

首先需要明确的是，我们讨论的是什么样的曲线。

椭圆曲线有比较复杂的定义: https://en.wikipedia.org/wiki/Elliptic_curve .而我们讨论的椭圆曲线比这个简单，它是以下方程所描述的一条 平滑曲线 :

$$y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0$$

它描述的并不是一个椭圆，之所以称它为"椭圆曲线方程"， 是因为它源自于求椭圆弧长的椭圆积分的反函数。椭圆曲线是无奇点的，即没有尖点，且不会自相交。当 $a,b$ 的值不同时，椭圆曲线会表现出不同的形态:

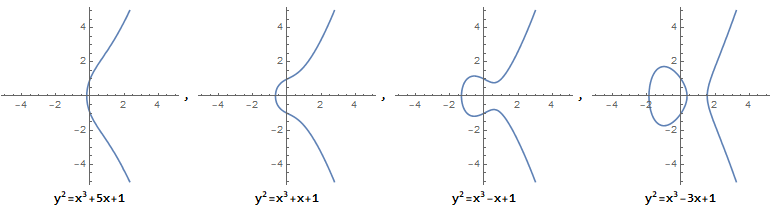
而当 $4a^3 + 27b^2 = 0$ 时， 它不是椭圆曲线：

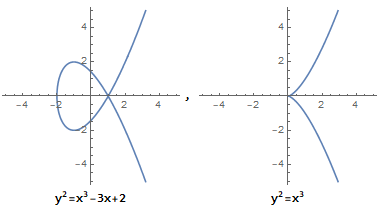
从图中可以看到，椭圆曲线总是 沿 x 轴对称 的。这是因为 $y^2$ 的存在。特殊地，我们规定 无穷远点 也存在于椭圆曲线上。我们用 $0$ 或符号 $O$ 来表示无穷远点，则椭圆曲线在实数域上的定义如下：

$$\{ (x,y) \in \mathbb{R}^2 | y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0 \} \cup \{0\}$$

和对称加密不同，公钥加密的密钥分为加密密钥(公钥)和解密密钥(私钥)。 公钥是公开的，任何人都有可能知道公钥，并用公钥生成密文，而私钥是保密的，只有解密者才能知道私钥，用它来解密密文获得明文。在这里对使用最广泛的公钥密码算法-- RSA.

RSA 是发明此算法的三位科学家的姓氏的首字母(吐槽一下：外国人的命名真随意)

RSA 加密

在RSA中，明文，密钥和密文都是数字， RSA的加密过程可以用如下公式表达：

$$\text{密文 = 明文}^E  \mod N$$

即： RSA  的密文是明文的 $E$ 次方求模 $N$ 的结果, 或者说，密文是明文的 $E$ 次方除以 $N$ 的余数。这就是整个加密过程，它非常简洁。因此，如果知道了 $E$ 和 $N$ ，那么任何人都可以进行加密运算，也就是说，$E$ 和 $N$ 是公钥.
在实际使用中， $E$ 和 $N$ 是经精心计算的数字。

在 C++11 之前 ，C++ 标准并没有提供统一的并发编程标准，也没有提供语言级别的支持。这导致我们在编写可移植的多线程程序时很不方便，往往需要面向不同的平台进行不同的实现，或者引入一些第三方平台，如Boost,pthread_win32 等。 从C++11开始 ，对并发编程进行了语言级别的支持，使用使用C++进行并发编程方便了很多。这里介绍C++11并发编程的相关特性。