Diffie-Hellman 密钥交换原理

在使用对称加密中，有一些无法避免的问题：

• 密钥如何从加密方传递给解密方。窃听者如果可以劫获密文，那么也可能劫获密钥.
• 如果窃听者破解了密钥，加密方如何将新的密钥安全地交给解密方

DH 密钥交换

解决上述问题的一种方法就是 DH 密钥交换 技术 。

DH 密钥交换全称为 Diffie-Hellman 密钥交换 ,是1976年由 Whitfiedl Diffle 和 Martin Hellman 共同发明的一种算法。使用这种方法，通信双方可以在窃听者眼皮子底下来安全地传输密码。

DH 交换的步骤如下：

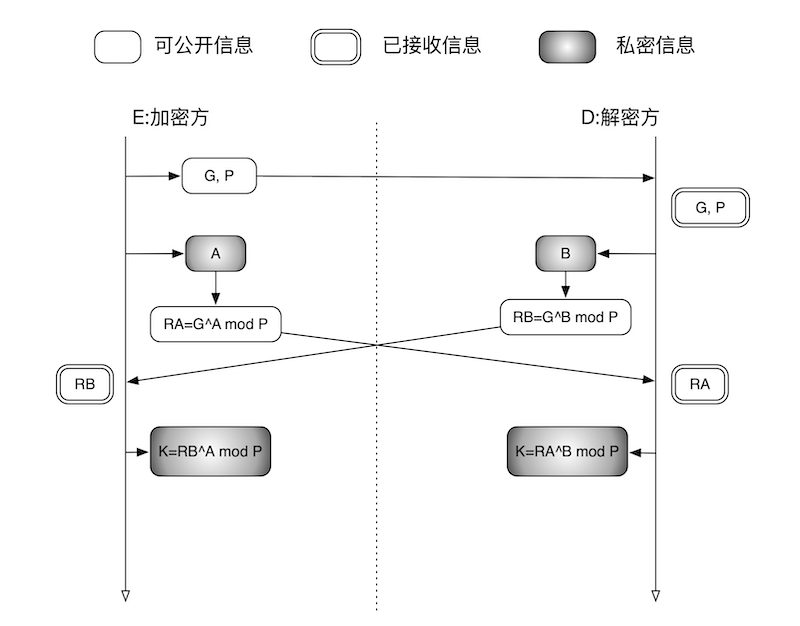
1. E 向 D 发送两个数 $G,P$ , $P$ 是一个非常大的质数，$G$ 是一个与 $P$ 相关的数，称为 生成元(generator) (这个概念在会后面讲到). $G$ 和 $P$ 不需要保密 。(其实这两个数也可以由 D 来生成)
2. E 生成随机数 $A$ $A$ 是一个介于 $1 \dots P-2$ 之间的数，这个数是只有 E 知道的私密数字
3. D 生成随机数 $B$ 同样，$B$ 也介于 $1 \dots P-2$, 且这个数只能由 D 知道
4. E 将 $RA = G^A \mod P$ 发送给 D $RA$ 是可以公开的
5. D 将 $RB = G^B \mod P$发送给 E 同样， $RB$ 可以公开
6. E 计算共享密钥 $KA = (G^B \mod P)^A \mod P = G^{B\times A} \mod P$
7. D 计算共享密钥 $KB = (G^A \mod P)^B \mod P = G^{A\times B} \mod P$

由此可以得出 $KA == KB$

DH交换的安全性

在上述步骤中，窃听者可以得到的信息有4 个： $P, G, G^A\mod P, G^B\mod P$ . 由这 4 个数字计算出 $G^{A\times B} \mod P$ 是非常困难的。要计算  $G^{A\times B} \mod P$  ，则要算出 $A \text{和} B$ 。如果知道 $G^A$ 算出 $A$ 并不难，而根据 $G^A \mod P$ 算出 $A$ 则是不可能的(当 $P$ 足够大时，至少在现在不可能)。 由 $G^A \mod P$ 计算 $A$  的问题称为 有限域上的离散对数问题， 其复杂度即是 DH 密钥交换的基础。

生成元

生成元是 数论 中的概念。如果整数 $g,p$ 满足 $\text{gcd}(g,p)=1$ (即 $g,p$ 互质), 那么根据欧拉定理， $g^x \equiv 1 \mod p$ 必然存在正整数解。若 $n$ 为所有解中的最小正整数，那么称 $n$ 是 $g \mod p$ 的阶,记作 $\text{ord}_p g = n$  。 对于整数 $p$， 存在正整数 $g$ 满足 $\text{ord}_p g = \varphi(p)$， 则称 $g$ 是 $p$ 的一个原根 ，也可以称 $g$ 是 $p$ 的一个生成元。
对于 群 $\mathbb(S,\oplus)$ , 存在 $g,a \in \mathbb{S}, \text{且} g \oplus a \text{生成集合} \mathbb{T}, \mathbb{S} = \mathbb{T}$ , 那么 $g$,即是 $\mathbb(S,\oplus)$ 的生成元。结合此文，$\mathbb{S}$ 即为与 $P$ 互质的有限域,即 $\{p | 1 \leqslant P \leqslant P-1\}$, $\oplus$ 即为 $\mod P$.

实践

1. E 选择质数 $P =13$, 生成元 $G = 2$ ,并发送给 D
2. E 生成随机数 A . 假如 A = 9
3. D 生成随机数 B, 假如 B = 7
4. E 发送RA 给 D, RA = $2^9 \mod 13 = 5$
5. D 发送RB 给 E, RB = $2^7 \mod 13 = 11$
6. E 算出 KA, KA = $RB^{A} \mod P = 11^9 \mod 13 = 8$
7. D 算出 KB, KB = $RA^{B}\mod P = 5^7 \mod 13 = 8$

通过上述步骤，E 和 D 都生成了共享密钥 8.