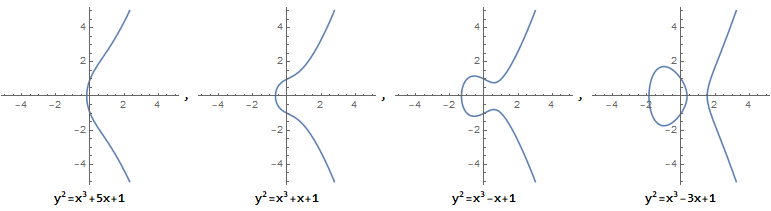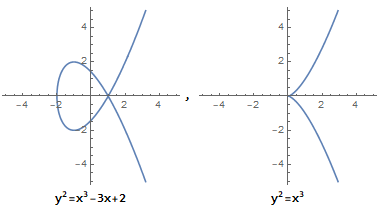ECC(Elliptic Curves Cryptography) 椭圆曲线加密原理

ECC(Elliptic Curves Cryptography) 属于非对称加密算法的一个重要组成部分。

本文尽量简单地阐述椭圆曲线加密的原理，但需要读者有一些初级的数论与离散数学相关的知识，或者推荐简单地阅读《算法导论》第31章:数论算法。

椭圆曲线

首先需要明确的是，我们讨论的是什么样的曲线。

椭圆曲线有比较复杂的定义: https://en.wikipedia.org/wiki/Elliptic_curve .而我们讨论的椭圆曲线比这个简单，它是以下方程所描述的一条 平滑曲线 :

$$y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0$$

它描述的并不是一个椭圆，之所以称它为"椭圆曲线方程"， 是因为它源自于求椭圆弧长的椭圆积分的反函数。椭圆曲线是无奇点的，即没有尖点，且不会自相交。当 $a,b$ 的值不同时，椭圆曲线会表现出不同的形态:

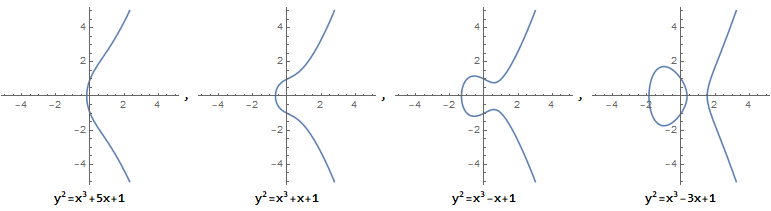
而当 $4a^3 + 27b^2 = 0$ 时， 它不是椭圆曲线：

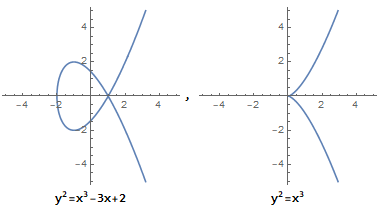
从图中可以看到，椭圆曲线总是 沿 x 轴对称 的。这是因为 $y^2$ 的存在。特殊地，我们规定 无穷远点 也存在于椭圆曲线上。我们用 $0$ 或符号 $O$ 来表示无穷远点，则椭圆曲线在实数域上的定义如下：

$$\{ (x,y) \in \mathbb{R}^2 | y^2 = x^3 + ax + b, 4a^3 + 27b^2 \neq 0 \} \cup \{0\}$$

椭圆曲线上的运算

加法运算

假设 $P(x_p,y_p), Q(x_q, y_q)$ 是椭圆曲线上的两点，我们来定义椭圆曲线上的二元运算 +：

1) 如果 $P \neq Q$, 且 $x_p \neq x_q$ ,则过 $P, Q$ 的直线会与椭圆曲线相交于第三点， 记作 $R_1, R_1$ , 沿 $x$ 轴的对称点记做 $R$, 定义 $P + Q = R$ . 同时可定义 取椭圆曲线上沿 $x$ 轴对称的点的操作为 - .即 $R_1 = -R$. 可知$P + Q - R = 0$。

2) 如果 $P \neq Q$ ,且 $yp = -yq$ (即 $P,Q$ 沿 $x$ 轴对称,过$P, Q$ 的直线垂直于 $x$ 轴), 则此时 $P + Q = 0$

3) 如果 $P = Q$, 过 $P$ 做椭圆曲线的切线，切线与椭圆曲线的另一个交点记作$R_1$, 令 $R = -R_1$, 则 $P + Q = P + P = 2P = R$

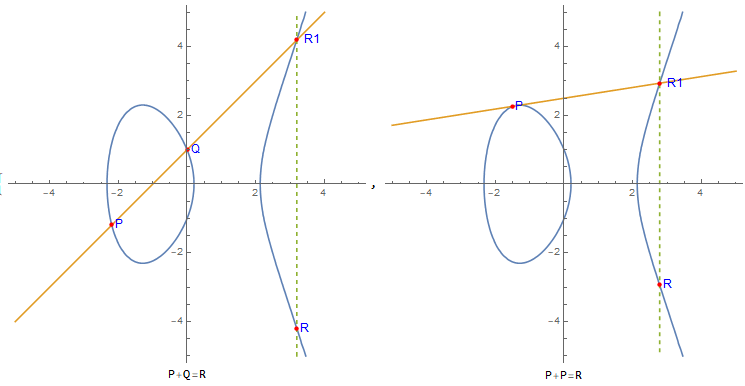
$+$ 运算的代数表示：

设椭圆曲线上点的集合为 $\mathbb{E} = \{(x,y) | y^2 = x^3 + ax+b, 4a^3 + 27b^2 \neq 0)\} \cup \{0\}$ ,且 $P(x_P,y_P), Q(x_Q, y_Q) \in \mathbb{E}$ ,  $P \neq 0, Q \neq 0$ , 有

• 若 $y_P \neq -y_Q$, 则 $R=P+Q$:

$$\begin{split} x_R &= m^2 -x_P - y_P \\ y_R &= y_P + m(x_R - x_P) \end{split}$$

,

$$m = \begin{cases} \frac{y_P - y_Q}{x_P - x_Q} & \text{if } x_P \neq x_Q \\ \frac{3x_P^2 + a}{2y_P} & \text{if } P = Q \end{cases}$$

-  若 $y_P = -y_Q$， $R = P + Q = 0$

$+$ 运算定义了椭圆曲线上的以 $0$ 为单位元的 群 。

标量乘法

在前面我们定义了椭圆曲线上的加法，其中有 $P + P = 2P$ , 同样地，我们定义椭圆曲线上的标量乘法：

若 $P$ 是椭圆曲线上的点，$n$ 是正整数，则

$$nP = \underbrace{P + P + \dots + P}_{n \text{个}}$$

根据定义计算 $nP$ 的过程如下：

$$\begin{equation} \begin{split} 2P & = P + P\\ 3P& = 2P + P\\ &\;\;\vdots \\ nP & = (n-1)P + P \end{split} \end{equation}$$

共需要计算 $n-1$ 次。这个算法的时间复杂度为$O(n)$ 下面来探讨一些更快捷的方法。

例如计算 $100P$ ,过程可以如下：

$$\begin{split}  2P & = P+P  \\ 4P & = 2P + 2P  \\ 8P & = 4P + 4P \\ 16P &= 8P + 8P \\ 20P &= 16P + 4P \\ 40P &= 20P + 20P \\ 80P &= 40P + 40P \\ 100P &= 80P + 20P \end{split}$$

这样 8 次即可算出 $100P$， 比前面的算法要简单。

过程还可以如下：

$$\begin{split} 100 &= 1100100_2 \\ &= 1\cdot 2^6 +1\cdot 2^5 + 0\cdot 2^4 + 0\cdot 2^3 + 1 \cdot 2^2 + 0 \cdot 2^1 + 0 \cdot 2^0  \end{split}$$

则：

$$\begin{split} 2^0P &=P \\ 2^1P &= 2^0P + 2^0P \\ 2^2P &= 2^1P +2^1P \\ 2^3P &= 2^2P + 2^2P \\ 2^4P &=2^3P + 2^3P \\ 2^5P &=2^4P + 2^4P \\ 2^6P &= 2^5P + 2^5P\\ \text{那么: } 96P &= 2^6P + 2^5P \\ 100P &= 96P + 2^2P \end{split}$$

这个算法中，求 $2^xP$的时间复杂度为$O(1)$, 所以整个的时间复杂度为 $O(\log_2 n)$ (或者为$O(k), k$ 为 $n$ 的二进制位数)。

有限域上的椭圆曲线

前面讨论的是椭圆曲线方程在实数域上的情况。接下来讨论椭圆曲线方程在质数有限域上的情况。 椭圆曲线在质数 $p$ 的有限域 $F_p$ 上的点的集合为:

$$\begin{aligned} \{ (x,y) \in (\mathbb{F}_p)^2  | y^2 \equiv x^3 + ax + b \pmod p, \\ 4a^3 + 27b^2 \not{\equiv} 0 \pmod p, a \in \mathbb{F}_p, b \in \mathbb{F}_p \} \cup \{0\}  \end{aligned}$$

此时的方程描述的不再是一条平滑曲线，而是 n 个离散点的集合。下图为椭圆曲线 $y^2 \equiv x^3 + x + 1 \pmod p, p=\{11,29,61,101\}$ 的图像：

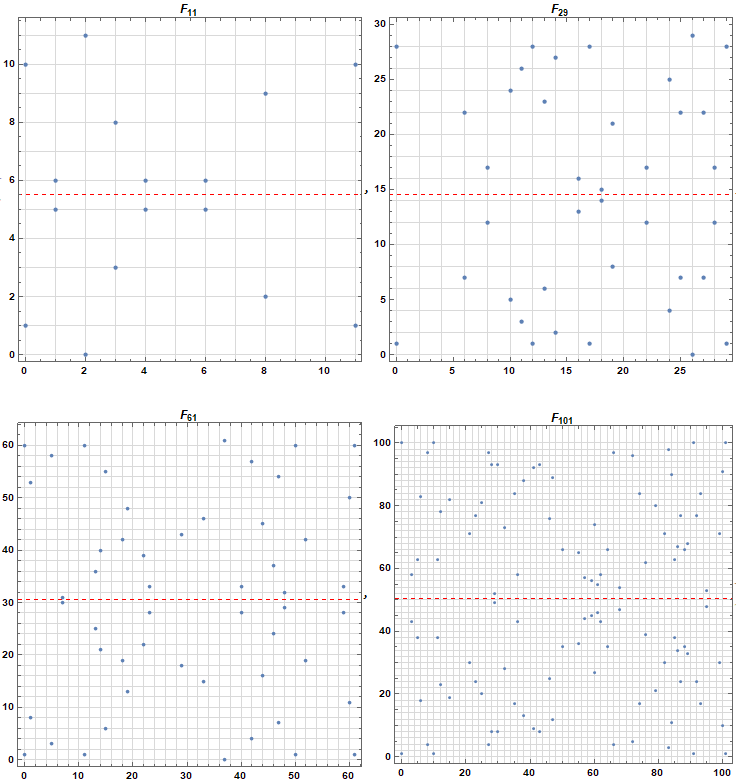
由图不难看出，这些点是关于 $P/2$ 对称的。

GFp 上的运算

前面我们定义了实数域上椭圆曲线两个点进行 $+$ 运算的几何意义，这个意义在有限域内依然是成立的。不同的是，这里的 “直线” 发生了变化, 它同样需要 $\pmod p$ 操作。 我们定义有限域上椭圆曲线两点相加的意义，

若 $P(px,py),Q(qx, qy)$ 有限域 $GF_p$ 上椭圆曲线的两点：

• 若 $px \neq qx$, 可以过两点 $P,Q$ 做直线，它将与椭圆曲线相交于第三点 $R_1, R_1$ 沿直线 $p/2$ 对称的点称为 $R$, 则 $R = -R_1 = P + Q$
• 若 $px = qx, py != qy$ , 则 $P + Q = 0$
• 若 $px = qx,  py = qy$, 这里我们无法给点做切线，暂且认为这个操作在几何上是无意义的。但它在代数上是可以计算的。

例如，当 $p=29$ 时，点 $P(0,1),Q(1,7)$ 在椭圆曲线 $y^2 \equiv x^3  +x + 1 \pmod p$ 上。此时 $R = P + Q$ 如下所示：

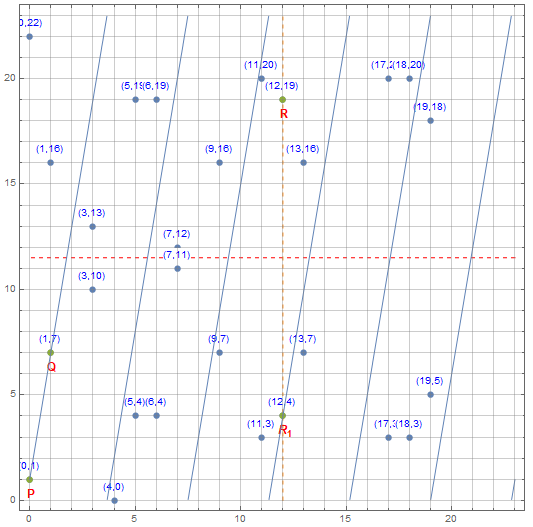
GFp 上的代数运算

有限域 $GF_p$上的代码运算和前面所讨论的实数域上的运算差不多，只不过多了 $\pmod p$ 运算。假设有限域上的椭圆曲线两点 $P(x_P, y_P),Q(x_Q, y_Q), R(x_R, y_R) = P + Q$,

1. 若 $y_P \neq -y_Q$,

$$\begin{split} x_R &= m^2 - x_P - y_P \pmod{p} \\ y_R &= y_P + m(x_R - x_P) \pmod{p} \end{split}$$

,

$$m= \begin{cases}  \frac{y_P-y_Q}{x_P-x_Q} \pmod p  &x_P \neq x_Q \\ \frac{3x_P^2+ a}{2y_P} \pmod p &x_P = x_Q \end{cases}$$

2. 若 $y_P = -y_Q$， $R = P + Q = 0$

注意这里的 $x^{-1} \pmod p$ 是对 $x$ 求模逆运算。

椭圆曲线的一些其它概念

在有限域内的椭圆曲线上具有有限个点，这些点构成一个有限交换群 $\mathbb{S}$，点的个数称为群的 序(order) ,一般用 $n$ 表示。计算群的序可以使用 “Schoof 算法”  https://en.wikipedia.org/wiki/Schoof’s_algorithm

以 $\mathbb{S}$ 上的一个点 $G$ 进行重复的加法运算， 能够生成一个子群 $\mathbb{S}^{'}$ . 群$\mathbb{S}^{'}$ 可能与群 $\mathbb{S}$ 相同， 也有可能是其真子群。群 $mathbb{S}$ 与 群 $\mathbb{S}^{'}$ 的比值称为 协因子 或 余因子(confactor),一般用 $h$ 表示， $h=\frac{|\mathbb{S}|}{|\mathbb{S}^{'}|}$ . 一般令 $h=1$, 此时群的阶最大，可用的点最多。$G$ 称为这个群的 生成元

椭圆曲线密码学中的离散对数问题

有限域 $GF_p$ 上的椭圆曲线 $\mathbb{E}$ 中的一点 $P$, 令 $R = kP, k<p$ .

已知 $k,P$, 计算$R$是很容易的，反过来已知$P,Q$, 求 $k$ 是困难的。目前已知的求 $k$的有效算法的复杂度为 $O(\sqrt{p})$

这就是椭圆曲线上的离散对数问题。故可以将 $Q$ 作为公钥，$k$ 作为私钥。