RSA 公钥加密原理

和对称加密不同，公钥加密的密钥分为加密密钥(公钥)和解密密钥(私钥)。 公钥是公开的，任何人都有可能知道公钥，并用公钥生成密文，而私钥是保密的，只有解密者才能知道私钥，用它来解密密文获得明文。在这里对使用最广泛的公钥密码算法-- RSA.

RSA 是发明此算法的三位科学家的姓氏的首字母(吐槽一下：外国人的命名真随意)

RSA 加密

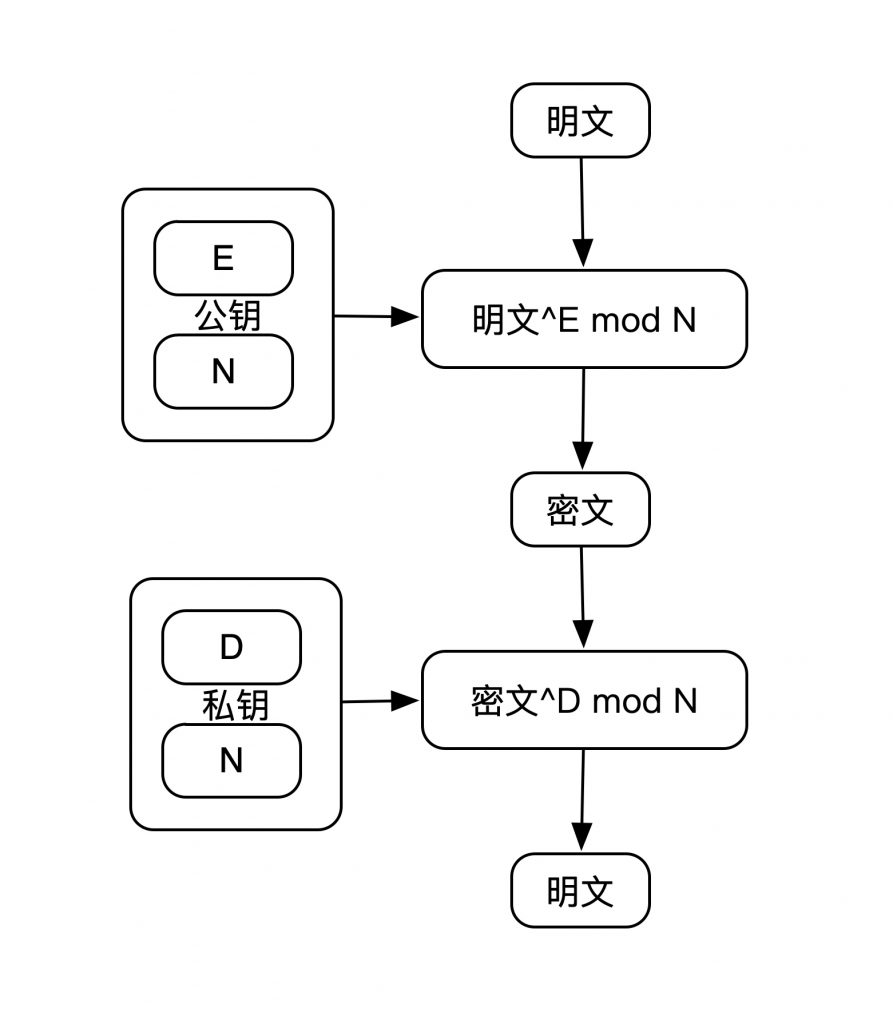
在RSA中，明文，密钥和密文都是数字， RSA的加密过程可以用如下公式表达：

$$\text{密文 = 明文}^E  \mod N$$

即： RSA  的密文是明文的 $E$ 次方求模 $N$ 的结果, 或者说，密文是明文的 $E$ 次方除以 $N$ 的余数。这就是整个加密过程，它非常简洁。因此，如果知道了 $E$ 和 $N$ ，那么任何人都可以进行加密运算，也就是说，$E$ 和 $N$ 是公钥.
在实际使用中， $E$ 和 $N$ 是经精心计算的数字。

RSA 解密

RSA 解密公式如下：

$$\text{明文} = \text{密文}^D \mod N$$

即，对密文的 $D$ 次方求模 $N$ 运算，就可以得到明文。这是里 $D$ 和 $N$ 是私钥

密钥对

刚刚提到， $E,D,N$ 是精心计算的数字。这三个数的组合，我们称之为 密钥对 .它们到底是如何生成的呢？

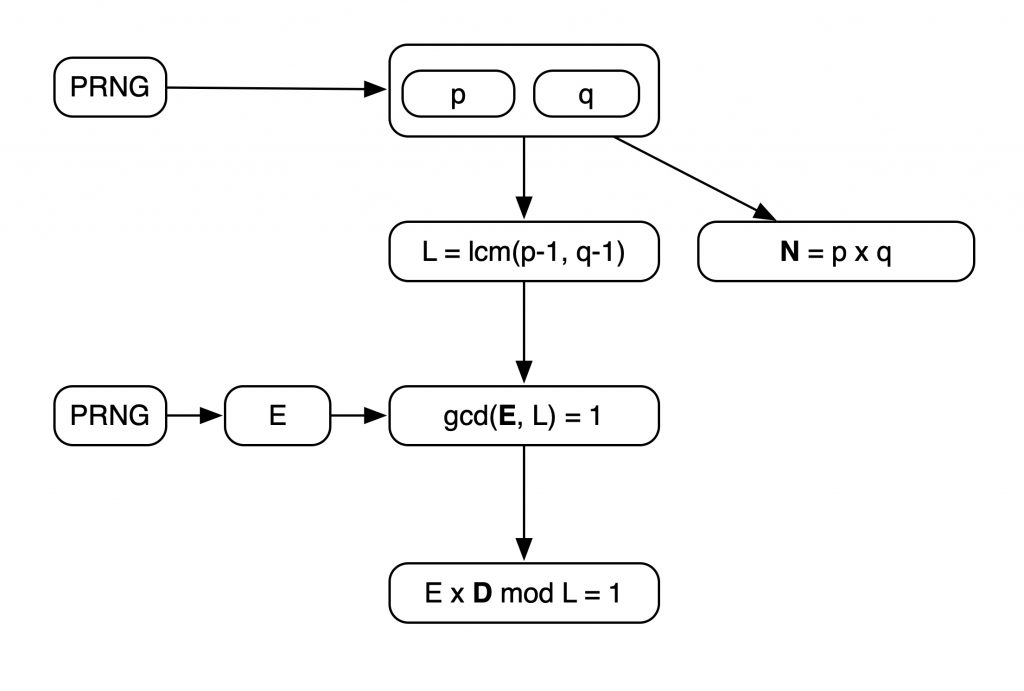
1 模数 N

有两个随机质数 $p,q$ ,它们必须大小合适：如果太小，密码就会很容易被破解，如果太大，计算的时间会变得很长。一般 $q$ 和 $p$ 都是512bit 大小，相当于 155 位的十进制数字。将这两个质数相乘，得到的就是 $N$ , 即：

$$N = p \times q  \qquad (p, q \text{为质数})$$

2 求 L

$L$ 不参与加解密的过程，它只出现在生成密钥对的过程中。 $L$ 是 $p-1$ 与 $q-1$ 的最小公倍数。设 lcm (least common multiple) 是求最小公倍数的方法，那么：

$$L = \text{lcm}(p-1,q-1)$$

3  求 E

$E$ 是一小于 $L$ 且与 $L$ 互质的随机数。

$$E \in(1, L), \text{且 gcd} (E,L) = 1$$

4 求 D

$D$ 由 $E$ 计算。$D, E, L$ 满足以下关系：

$$D\in(1,L)\ \text{且}\ E\times D\ \text{mod}\ L = 1$$

参考第 3 条， $E\times D\ \text{mod}\ \ L = 1$ 保证了对密文解密时能得到明文。

RSA 的机密性

由前面的介绍可以知道， RSA 加解密就是简单的求$x$次方再求模的运算，原理非常简单，它的机密性如何呢？或者说，如何来破解 RSA 加密呢？

破解者可以知道信息有：

• 密文
• 公钥 $E,N$

不知道的信息有

• 明文
• $D$

假如一个黑客想破解 RSA, 他可能用到哪些方法？

通过密文求明文

模运算使由密文求明文变成了求离散对数的问题。目前人类还没有发现求离散对数的高效算法

求解 D

知道 $D$ 就可以知道密钥。现在 RSA 中使用的 $p$ 与 $q$ 的长度都在1024 bit 以上，$N$的长度在 2048 bit 以上。暴力破解基本上是不可能的。

能否通过 $E, N$ 求出 $D$呢， 毕竟 $D$ 是使用 $E, L$ 算出来的，对 $L$ 的计算又涉及到了 $p,q$ , 只要知道 $p ,q$ 就能知道 $D$ 了。黑客还知道 $N = p \times q$ , $p$ 和 $q$ 都是质数，到此破解问题归结为对 $N$ 进行 质因数分解问题 。然而，目前人类还没有发现对大整数进行质因数分解的高效算法(甚至都不知道是否存在一种分解质因数的简单方法)

最简单的方法，就是通过破解伪随机数生成器 “PRNG” 的算法了。如果 PRNG 的算法很差，那么黑客就有可能推测出 $p,q$。这个问题已经超出了 RSA 算法的本身，转变成了伪随机数算法问题，此处不予讨论。

RSA 算法的本质， 就是 对大数求质因数分解的十分困难 这一数学问题。

大数要多大才安全？

无数大数 $N$ 有多长，只要持续地去算，总有一天能够多被质因数分解。随着计算能力的提升，质因数分解所需要的时间会逐步缩短。有一些组织会将算出的 $N$ 与 $p,q$ 公布出来。随着技术进步，以前被认为是安全的密码都将会被一一破解。这一现象称为 密码劣化 。 基于此， NIST SP800-57 给出如下建议：

• 1024 bit 的 RSA 不因再被使用
• 2048 bit 的 RSA 可以使用至 2030 年
• 4096 bit 的 RSA 在2030年以后仍可以使用一段时间

其它公钥加密方法

公钥加密除了 RSA， 还有一些其它的算法, 比如：

• Elgamal
• Rabin
• 椭圆曲线密码

其它

RSA 的例子

有随机质数 $p,q$， 假设 $p = 61, q = 53$

$N = p \times q = 61 \times 53 = 3233$

$L = \text{lcm}(p-1, q-1) = 780$

有随机数 $E \in(1, L)$ ,且 $E,L$  互质。假设 $E=17$

计算 $D=413$, $413 \times 17 = 1 \ \text{mod}\ 780$

那么公钥为 $(E, N) = (17, 3233 )$, 私钥为 $(D, N) = (413, 3233)$

至此，假设有明文消息 $M = 65$:

密文 $C = 65 ^ {17} \ \text{mod} \ 3233 = 2790$

明文 $M = 2790 ^ {413} \ \text{mod} \ 3233 = 65$

公钥加密与对称加密谁更安全

对称加密通过将明文进行复杂的形式转换来保证其机密性，密钥加密则是基于数学上的困难来保证其机密性。它们源于两种不同的思路，使用于不同的场景，无法比较。对于同一种加密思想，其机密性由密钥的长度决定、算法的强度等决定。下表展示了在算法强度相对均衡的情况下，具备同等抵御暴力破解强度的密钥长度比较：

AES   RSA
128  3072
192  7680
256  15360

在保证对称加密与公钥加密的机密性大致相等的情况下，公钥加密的处理速度更慢(只有对称加密的几百分之一)。因此，公钥加密并不适合用来对很长的消息进行加密。